01 矩阵

二叉树

红黑树

压缩列表(ziplist)

ziplist是一个经过特殊编码的双向链表，它的设计目标是节省内存。它可以存储字符串或者整数。其中整数是按二进制进行编码的，而不是字符串序列。

它能以O(1)的时间复杂度在列表的两端进行push和pop操作。但是由于每个操作都 u 要对ziplist所使用的内存进行重新分配，所以实际操作的复杂度与ziplist占用的内存大小有关。

在redis中，有序集合、散列和列表都直接或间接使用了压缩列表。当有序集合或散列的元素个数较少，并且元素都是短字符串时，redis便会使用压缩列表作为底层数据存储。redis的列表使用的快速链表数据结构进行存储，而快速链表就是双向链表与压缩列表的组合。

总的来说，ziplist有如下特性：

• 本质上是一个字节数组
• 是redis为了节约内存而设计的一种线性结构
• 可以包含多个元素，每个元素可以是一个字节数组或一个整数

在redis中，压缩列表主要由 5 部分组成：

属性	类型	长度	用途
zlbytes	unit32_t	4字节	记录整个压缩列表占用的内存字节数：在对压缩列表进行内存重分配，或者计算 zlend 的位置时使用。
zltail	unit32_t	4字节	记录压缩列表表尾节点距离压缩列表的起始地址有多少字节：通过这个偏移量，程序无需遍历整个压缩列表就可以确定表尾节点的地址。
zllen	unit16_t	2字节	记录了压缩列表包含的节点数量，当这个属性的值小于 UINT16_MAX（65535）时，这个属性的值就是压缩列表包含节点的数量；当这个值等于 UINT16_MAX 时，节点的真实数量需要遍历整个压缩列表才能计算得出。
entry	列表节点	不定	压缩列表包含的各个节点
zlend	unit8_t	1字节	特殊值 0xFF（十进制 255），用于标记压缩列表的末端。

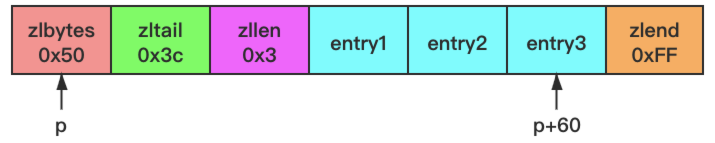
如上图所示，这是一个包含三个节点的压缩列表的示例：

• zlbytes 属性的值为 0x50（十进制 80），表示压缩列表的总长为 80 字节。
• zltail 属性的值为 0x3c（十进制 60），这表示如果我们有一个指向压缩列表起始地址的指针 p，那么只要用指针 p 加上偏移量 60，就可以计算出表尾节点 entry3 的地址。
• zllen 属性的值为 0x3（十进制 3），表示压缩列表包含三个节点。

对于压缩列表而言，每个entry的数据结构又包含三部分，分别是：

• previous_entry_length:表示前一个元素的长度，占 1 字节或者 5 字节
  • 当前一个元素的长度小于 254 字节时，使用 1 字节表示记录上一个元素长度
  • 当前一个元素的长度大于或等于 254 字节时，用 5 字节表示。其中第一个字节固定为0xFE(十进制为 254)，后 4 字节才是上一个元素的真正长度
• encoding：当前元素的编码，记录节点的content字段锁保存的数据的类型以及长度，它的类型一共有两种，分别是字节数组和整数。它的长度可能为 1字节、2 字节或者 5 字节
• content：用于保存当前节点的内容，节点内容类型和长度由encoding决定

encoding内容说明

当content要存储的数据是字节数组时:

内容	长度	描述
00 bbbbbb	1字节	最大长度为 63 的字节数组
01 bbbbbb xxxxxxxx	2字节｜最大长度 2^14-1的字节数组
10 ________ aaaaaaaa bbbbbbbb cccccccc dddddddd	5字节	最大长度2^32-1的字节数组

当content要存储的数据是整数时：

内容	长度	描述
11000000	1字节	int16_t类型整数(2字节)
11010000	1字节	int32_t类型整数(4字节)
11100000	1字节	int64_t类型整数(8字节)
11110000	1字节	24位有符号整数(3字节)
11111110	1字节	8 位有符号整数(1字节)
1111xxxx	1字节	用xxxx思维表示内容，此时将不在需要content
11111111	1字节	表示压缩列表的结束

跳跃表(zSkiplist)

跳跃表即跳表，是一个可以快速查询有序连续元素的数据链表。跳表的平均查找和插入时间复杂度都是O(long n)，优于普通队列的O(n)。

它最大的优势是原理简单、容易实现、方便扩展、效率更高。因此在一些热门的项目中用来替代平衡树，它最典型的用途就是作为redis中的zset的基础数据类型。

跳表是在链表的基础上，增加了多级索引，通过索引位置的几个跳转，实现数据的快速定位。

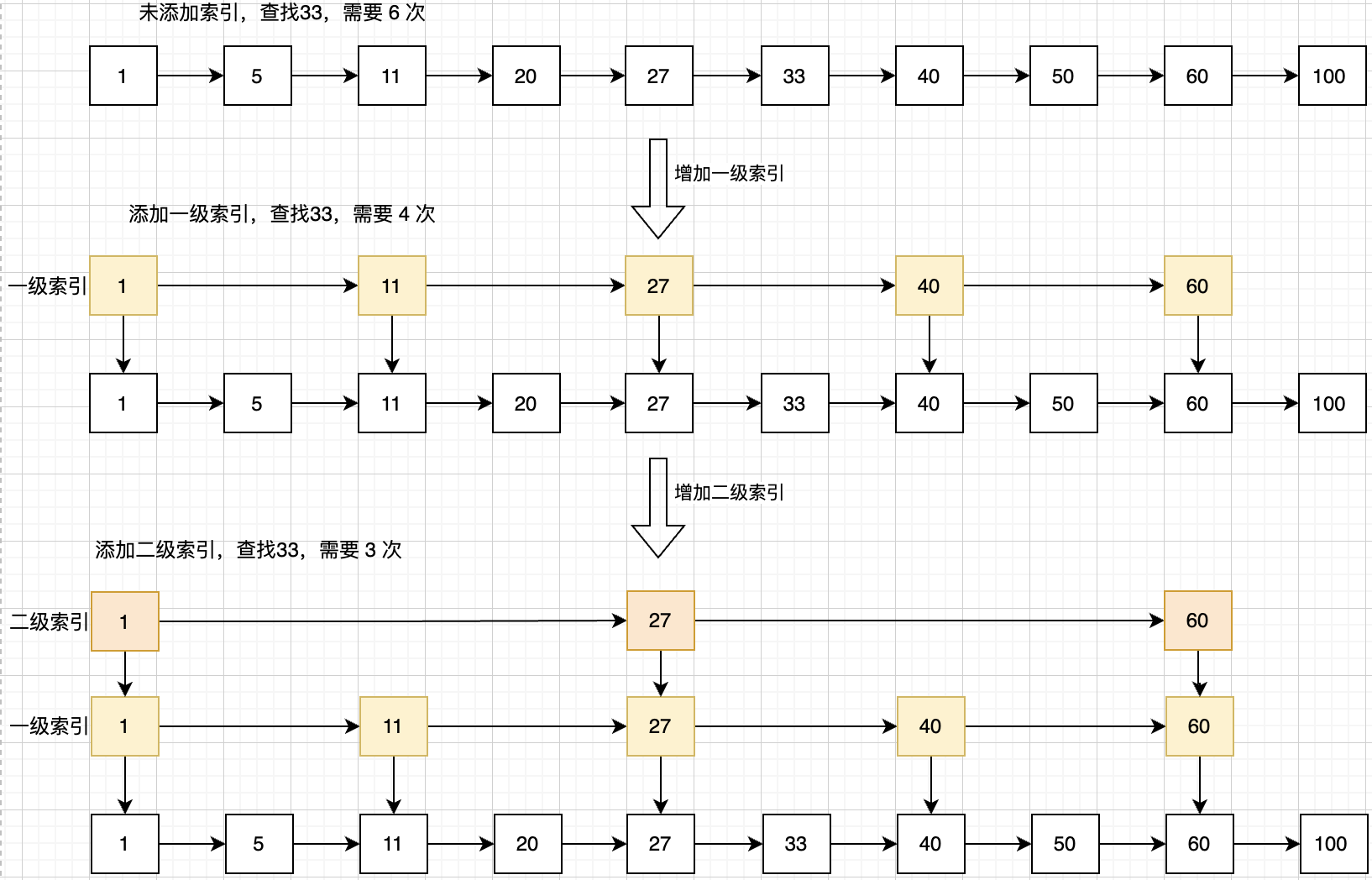
由上图可见，针对存储的数据个数，增加多级索引，查找数据时，按照多级索引，一级一级地以此查找，从而缩短查询的时间，当定位到原始链表后，如果没有查找到对应的值，那么也可以说明这个有序链表中不存在这个元素。

跳表查询的时间复杂度计算：

n/2、n/4、n/8、第 k 级索引结点的个数就是 n/(2^k)

假设索引有 h 级，最高级的索引有 2 个结点。n/(2^h) = 2，从而求得 h = log2(n)-1

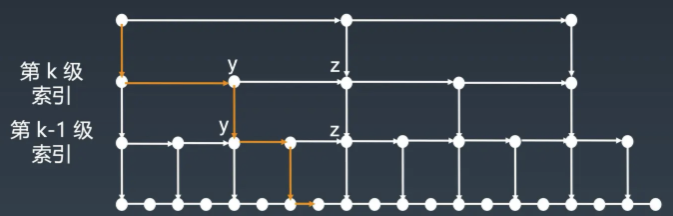
举一个例子，跳表在查询的时候，假设索引的高度：logn，每层索引遍历的结点个数：3，假设要走到第 8 个节点。

每层要遍历的元素总共是3个，所以这里的话 log2 8 的话，就是它的时间复杂度。最后的话得出证明出来：时间复杂度为log2n。也就是从最朴素的原始链表的话，它的 O(n) 的时间复杂度降到 log2n 的时间复杂度。这已经是一个很大的改进了。假设是1024的话，你会发现原始链表要查1024次最后得到这个元素，那么这里的话就只需要查（2的10次方是1024次）十次这样一个数量级。

跳表的空间复杂度计算：

假设它的长度为 n，然后按照之前的例子，每两个节点抽一个做成一个索引的话，那么它的一级索引为二分之 n 对吧。最后如下：

原始链表大小为 n，每 2 个结点抽 1 个，每层索引的结点数:  n/2,n/4,n/8,……,8,4,2

原始链表大小为 n，每 3 个结点抽 1 个，每层索引的结点数:  n/3,n/9,n/27,……,9,3,1

空间复杂度是 O(n)

跳表的构成

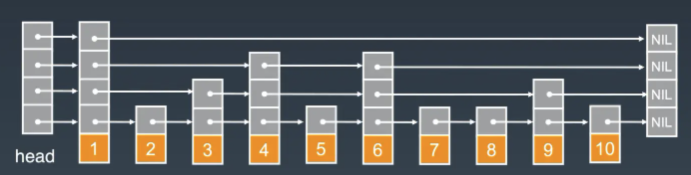
从图中可以看到， 跳跃表主要由以下部分构成：

• 表头（head）：负责维护跳跃表的节点指针。
• 跳跃表节点：保存着元素值，以及多个层。
• 层：保存着指向其他元素的指针。高层的指针越过的元素数量大于等于低层的指针，为了提高查找的效率，程序总是从高层先开始访问，然后随着元素值范围的缩小，慢慢降低层次。
• 表尾：全部由 NULL 组成，表示跳跃表的末尾。

用java实现跳表

参考链接

import java.util.concurrent.ThreadLocalRandom;

/**
 * 跳跃表实现
 */
public class SkipLists<Key extends Comparable<Key>, Value> {

    public static final int MAX_LEVEL = 32;

    private static final Object BASE_OBJECT = new Object();

    private static final int PROBABILITY = 50;

    private volatile HeaderIndex<Key, Value> header;


    public SkipLists() {
        this.header = new HeaderIndex(new Node(null, BASE_OBJECT, null), null, null, 1);
    }

    /**
     * 根据key从跳跃表中获取一个值
     * @param key key
     * @return 存在则返回对应的value，不存在则返回null
     */
    public Value get(Key key) {
        // 参数检查
        if (key == null) {
            throw new IllegalArgumentException();
        }

        // 找到key对应的前驱节点
        Node<Key, Value> predecessor = findPredecessor(key);
        // 从前驱节点开始遍历查找key对应的节点
        for (Node<Key, Value> next = predecessor.next;;) {
            if (next == null) {
                break;
            }

            // key与节点的Key比较
            // 如果相等就找到了直接返回值
            // 如果key大于节点的key，继续向后查找
            // 如果key小于节点的key，那么没找到，退出循环
            int cmp = key.compareTo(next.key);
            if (cmp == 0) {
                return next.value;
            } else if (cmp > 0) {
                next = next.next;
            } else {
                break;
            }
        }

        return null;
    }

    /**
     * 向跳跃表添加一个key-value对
     * @param key key
     * @param value value
     */
    public void put(Key key, Value value) {
        if (key == null) {
            throw new NullPointerException();
        }

        Node<Key, Value> newNode = null;
        // 找到最底层插入节点的前驱节点
        Node<Key, Value> predecessor = findPredecessor(key);

        // 找到索引节点对应的数据节点以后，开始查找插入数据前驱节点
        for (Node<Key, Value> b = predecessor, next = b.next;;) {
            if (next != null) {
                // 如果插入的key大于当前数据节点，那么继续查找下一个
                int cmp = key.compareTo(next.key);
                if (cmp > 0) {
                    b = next;
                    next = next.next;
                    continue;
                } else if (cmp == 0) {
                    next.value = value;
                    break;
                }
            }

            // 新建节点并更改前驱节点的下一个节点为新节点
            newNode = new Node<>(key, value, next);
            b.next = newNode;
            break;
        }

        // 是否要为数据节点添加索引层
        int level = randomLevel();

        // 需要加层
        if (level > header.level) {
            int oldLevel = header.level;
            int newLevel = level;

            // 为新节点创建索引节点
            Index<Key, Value>[] newNodeIndexes = createNewNodeIndex(newNode, newLevel);
            // 为头结点增量补充索引节点,并将头结点的索引节点指向新节点的索引节点
            header = incrHeaderIdxes(newLevel, newNodeIndexes);

            // 根据老层更新新节点的数据
            updateIndex(key, newNodeIndexes[oldLevel], oldLevel, newLevel);
        } else {
            // 如果节点索引层大于1就需要为节点新建索引层
            if (level > 1) {
                // 根据新节点索引层新建节点索引
                Index<Key, Value>[] newNodeIndexes = createNewNodeIndex(newNode, level);
                // 更新索引
                // 在没有新建层时，为新节点新建层传入的新层参数是头索引的层数，因为每次都从头索引开始查找，
                // 需要将头索引直接下降到对应的层后开始修改关系
                updateIndex(key, newNodeIndexes[level], level, header.level);
            }
        }
    }

    /**
     * 根据key删除一个节点
     * 注意删除节点可能需要减层
     * @param key 要删除的关键字
     * @return key对应的value值，如果没有找到value就返回null
     */
    public Value delete(Key key) {
        if (key == null) {
            throw new NullPointerException();
        }

        Value val = null;

        // 找到最底层插入节点的前驱节点
        Node<Key, Value> predecessor = findPredecessor(key);
        for (Node<Key, Value> b = predecessor, next = b.next;;) {
            if (next != null) {
                // 如果插入的key大于当前数据节点，那么继续查找下一个
                int cmp = key.compareTo(next.key);
                if (cmp > 0) {
                    b = next;
                    next = next.next;
                    continue;
                } else if (cmp < 0) {
                    break;
                } else {
                    // 相等就将节点元素设置为空
                    val = next.value;
                    next.value = null;
                    break;
                }
            }

            break;
        }

        // 通过查找前驱索引节点删除可能需要删除的索引
        // 删除索引的标记信息就是node.value==null
        findPredecessor(key);
        // 删除层
        // 如果头索引的右侧索引已经被删除就减层
        while (header.right == null && header.level > 1) {
            header = (HeaderIndex<Key, Value>) header.down;
        }

        return val;
    }

    /**
     * 查找key对应的前驱索引
     * @param key key
     * @return 前驱索引
     */
    private Index<Key, Value> findIndex(Key key) {
        for (Index<Key, Value> cur = header, right = cur.right, down;;) {
            // 如果索引的右侧不为空
            // 用搜索的key对数据节点的key进行比较
            // 如果搜索的key大于索引节点的key，那么继续向右进行搜索
            if (right != null) {
                Node<Key, Value> n = right.node;
                Key k = n.key;
                // value为空代表节点的值已经被删除
                // 删除节点对应的索引
                if (n.value == null) {
                    // 将当前所有的右侧索引更新为右侧的右侧
                    cur.right = right.right;
                    // 更新right索引变量为当前索引的右侧
                    right = cur.right;
                    continue;
                }

                // 如果搜索的key大于右侧节点指向的key，那么继续向右查找
                if (key.compareTo(k) > 0) {
                    cur = right;
                    right = right.right;
                    continue;
                }
            }

            // 如果索引节点的右侧节点大于key，那么向下放索引查找
            if ((down = cur.down) != null) {
                // 将当前节点指向下方索引节点
                // 右侧节点指针指向下方索引的右侧
                cur = down;
                right = down.right;
            } else {
                return cur;
            }
        }
    }

    /**
     * 查找key对应的前驱节点
     * @param key key
     * @return 前驱节点
     */
    private Node<Key, Value> findPredecessor(Key key) {
        Index<Key, Value> index = findIndex(key);
        return index.node;
    }

    /**
     * 更新老层的索引
     * @param key 关键字
     * @param newNodeOldIdx 新节点索引
     * @param oldLevel 老层数
     * @param newLevel 新层数
     */
    private void updateIndex(Key key, Index<Key, Value> newNodeOldIdx, int oldLevel, int newLevel) {
        Index<Key, Value> newNodeIdx = newNodeOldIdx;
        Index<Key, Value> precursorIdx = header;

        // 跳过新索引层，因为已经做了关联
        for (int i = oldLevel + 1; i <= newLevel; i++) {
            precursorIdx = precursorIdx.down;
        }
        Index<Key, Value> right = precursorIdx.right;

        // 找到对应的层之后，我们开始向右继续查找前驱索引节点
        while (true) {
            if (right != null && right.node.value != null) {
                int cmp = key.compareTo(right.node.key);
                if (cmp > 0) {
                    precursorIdx = right;
                    right = right.right;
                    continue;
                }
            }

            // 找到需要更新的索引之后，重建索引
            // 前驱索引节点的右侧设置新的索引
            precursorIdx.right = newNodeIdx;
            // 新索引有右侧设置为老索引的右侧节点
            newNodeIdx.right = right;
            // 新节点索引向下
            newNodeIdx = newNodeIdx.down;
            // 老索引向下
            precursorIdx = precursorIdx.down;
            if (precursorIdx == null) {
                break;
            }
        }
    }

    /**
     * 随机生成节点的层，但是不超过32
     * @return 新节点层数
     */
    private int randomLevel() {
        int level = 1;
        int rnd = ThreadLocalRandom.current().nextInt(1, 101);
        while (rnd > PROBABILITY && level <= MAX_LEVEL) {
            // 根据随机数来生成索引层数
            ++level;
            rnd = ThreadLocalRandom.current().nextInt(1, 101);
        }
        return level;
    }

    /**
     * 为头结点补充索引层级
     * @param newLevel 新层数
     * @param newNodeIdxes 新节点索引数组
     * @return 新的头结点
     */
    private HeaderIndex<Key, Value> incrHeaderIdxes(int newLevel, Index<Key, Value>[] newNodeIdxes) {
        HeaderIndex<Key, Value> newHeader = header;
        for (int i = header.level + 1; i <= newLevel; i++) {
            newHeader = new HeaderIndex<>(header.node, newHeader, newNodeIdxes[i], i);
        }

        return newHeader;
    }

    /**
     * 为新节点创建索引节点，并建立向下的索引关系
     * @param newNode 新节点
     * @param newLevel 层数
     * @return 新节点的索引节点
     */
    private Index<Key,Value>[] createNewNodeIndex(Node<Key,Value> newNode, int newLevel) {
        Index<Key,Value>[] newNodeIdxes = new Index[newLevel + 1];
        Index<Key,Value> newIndex = null;
        for (int i = 1; i <= newLevel; i++) {
            newIndex = new Index<>(newNode, newIndex, null);
            newNodeIdxes[i] = newIndex;
        }

        return newNodeIdxes;
    }

    /**
     * 数据节点
     */
    static class Node<Key, Value> {

        /**
         * 键
         */
        final Key key;

        /**
         * 值
         */
        volatile Value value;

        /**
         * 链表指针
         */
        volatile Node<Key, Value> next;

        public Node(Key key, Value value, Node<Key, Value> next) {
            this.key = key;
            this.value = value;
            this.next = next;
        }
    }

    /**
     * 索引
     */
    static class Index<K,V> {
        final Node<K,V> node;
        volatile Index<K,V> right;
        volatile Index<K,V> down;

        public Index(Node<K,V> node, Index<K,V> down, Index<K,V> right) {
            this.node = node;
            this.right = right;
            this.down = down;
        }
    }

    /**
     * 头
     */
    static class HeaderIndex<K,V> extends Index<K,V> {
        private final int level;

        public HeaderIndex(Node<K,V> node, Index<K,V> down, Index<K,V> right, int level) {
            super(node, down, right);
            this.level = level;
        }
    }
}

redis跳表的实现

Redis 的跳跃表由 redis.h/zskiplistNode 和 redis.h/zskiplist 两个结构定义， 其中 zskiplistNode 结构用于表示跳跃表节点， 而 zskiplist 结构则用于保存跳跃表节点的相关信息， 比如节点的数量， 以及指向表头节点和表尾节点的指针， 等等。

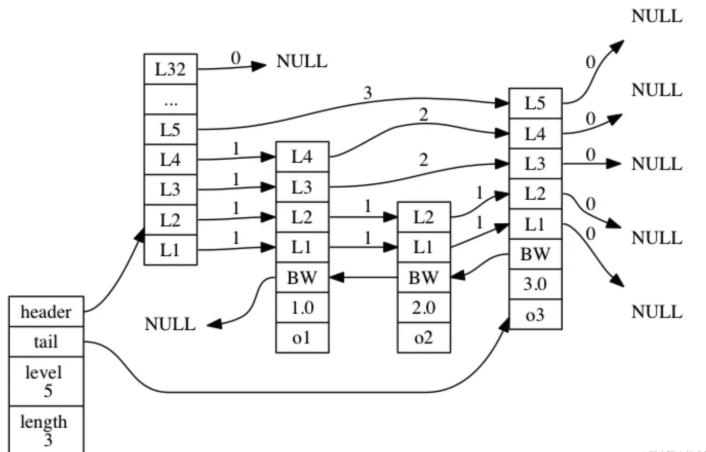
上图展示了一个跳跃表示例，位于图片最左边的示 zskiplist 结构，该结构包含以下属性：

• header ：指向跳跃表的表头节点。
• tail ：指向跳跃表的表尾节点。
• level ：记录目前跳跃表内，层数最大的那个节点的层数（表头节点的层数不计算在内）。
• length ：记录跳跃表的长度，也即是，跳跃表目前包含节点的数量（表头节点不计算在内）。

位于 zskiplist 结构右方的是四个 zskiplistNode 结构， 该结构包含以下属性：

• 层（level）：节点中用 L1 、 L2 、 L3 等字样标记节点的各个层， L1 代表第一层， L2 代表第二层，以此类推。每个层都带有两个属性：前进指针和跨度。前进指针用于访问位于表尾方向的其他节点，而跨度则记录了前进指针所指向节点和当前节点的距离。在上面的图片中，连线上带有数字的箭头就代表前进指针，而那个数字就是跨度。当程序从表头向表尾进行遍历时，访问会沿着层的前进指针进行。
• 后退（backward）指针：节点中用 BW 字样标记节点的后退指针，它指向位于当前节点的前一个节点。后退指针在程序从表尾向表头遍历时使用。
• 分值（score）：各个节点中的 1.0 、 2.0 和 3.0 是节点所保存的分值。在跳跃表中，节点按各自所保存的分值从小到大排列。
• 成员对象（obj）：各个节点中的 o1 、 o2 和 o3 是节点所保存的成员对象。

参考链接：https://juejin.cn/post/6893072817206591496