零钱兑换
题目
题目地址:https://leetcode-cn.com/problems/coin-change
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例1:
1
2
3
| 输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
|
示例2:
1
2
| 输入: coins = [2], amount = 3
输出: -1
|
答案
该题可以利用动态规划的算法思想来实现,首先明确动态规划的三个要点:最优子结构、状态转移方程、重叠子问题。
首先,在该题中,需要求解的是求得凑得指定金额(amount)所需要的最少硬币数,我们把这个称为原问题,例如示例1中,需要得出金额为11的最少硬币数,我们把这个称为子问题,比如现在我们有一枚1块的硬币,然后就可以转换为,得出金额为10的最少硬币数,我们把这个数成为数a,然后金额为11的最少硬币数就为数a + 1,因为每一个原问题都能转成若干个子问题,并且子问题之间不糊就相互制约,所以说该题是符合最优子结构的。
然后需要确定的就是状态转移方程,状态其实是原问题和子问题中的变化的变量,即每次变化金额amount,当然这里硬币的数量也是变化的,但是题意中,硬币是无限制的,所以硬币的个数不能作为该题的状态。
最后是重叠子问题,在研究本题的重叠子问题之前,我们先根据上述的状态转移方程来看看下面的图片:
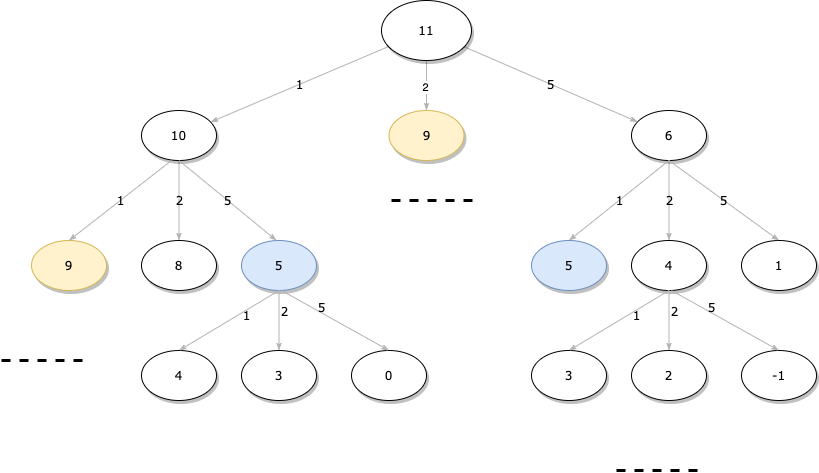
注:该图根据示例1绘制;图中的省略号为省略了后续的节点。
从图中不难看出,9、5刚好是两个重叠问题,如果输入的样例足够多,那么重叠项将会非常之多,解决了这类重叠问题,将能为程序节省很多的运行时间。
递归实现
使用递归实现,在分解每个子问题的时候,都传入一个新的方法里进行计算,同时增加一个temp变量,以解决重叠子问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
public int coinChange(int[] coins, int amount) {
return ccRec(coins, amount, new HashMap<>());
}
private int ccRec(int[] coins, int amount, Map<Integer, Integer> temp) {
if (amount == 0) {
return 0;
} else if (amount < 0) {
return -1;
}
Integer amountVal = temp.get(amount);
if (amountVal != null) {
return amountVal;
}
Integer res = null;
for (int i = 0; i < coins.length; i++) {
int coin = coins[i];
int ccRes = ccRec(coins, amount - coin, temp);
if (ccRes == -1) {
continue;
}
if (res == null) {
res = 1 + ccRes;
} else {
res = Math.min(res, 1 + ccRes);
}
}
res = res == null ? -1 : res;
temp.put(amount, res);
return res;
}
|
数据迭代实现
使用数组实现,定义一个dp数组来处理重叠子问题,数组的每个下标都代表着一个子问题,例如,dp[10]的值为凑成金额为10所需的硬币数。即:dp[i] = x表示,当目标金额为i时,至少需要x枚硬币。通过下面的图,应该能轻松理解。
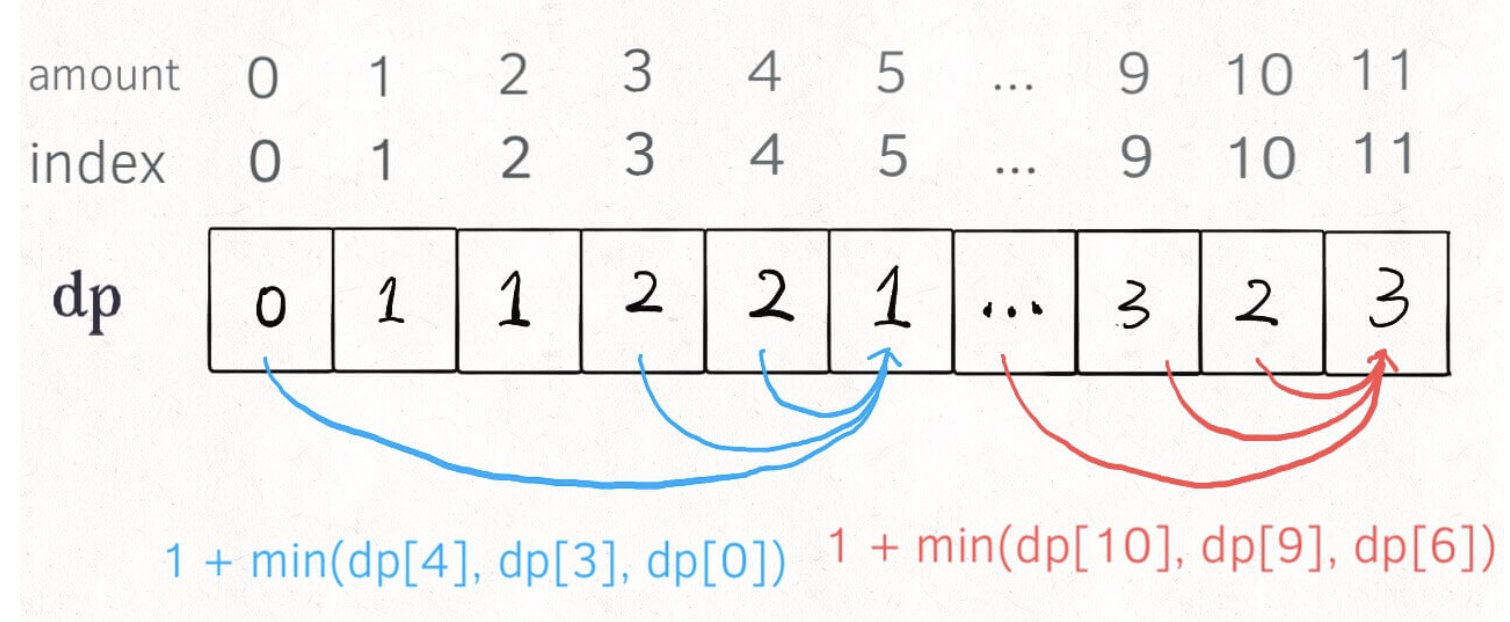
由于,金额可能会传入0,所以数组的长度为amount+1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public int coinChangev(int[] coins, int amount) {
Integer[] dp = new Integer[amount + 1];
dp[0] = 0;
for (int i = 1; i < dp.length; i++) {
for (int j = 0; j < coins.length; j++) {
int coin = coins[j];
int sub = i - coin;;
if (sub < 0 || dp[sub] == -1) {
continue;
}
if (dp[i] == null) {
dp[i] = 1 + dp[sub];
} else {
dp[i] = Math.min(dp[i], 1 + dp[sub]);
}
}
if (dp[i] == null) {
dp[i] = -1;
}
}
return dp[amount];
}
|