动态规划之简单(0-1)背包问题

动态规划的经典题目背包问题，今天尝试解答了一下，现总结如下。

题目描述

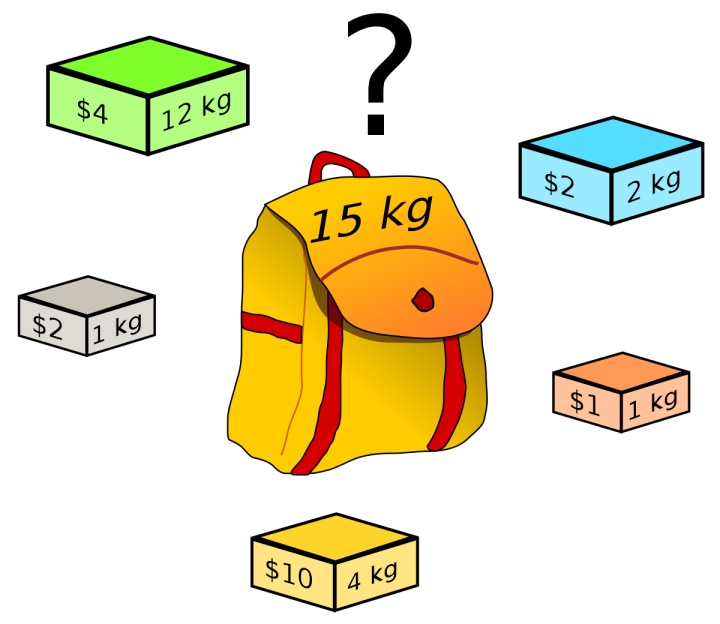
给你一个可装载重量为W的背包和N个物品，每个物品有重量和价值两个属性。其中第i个物品的重量为wt[i]，价值为val[i]，现在让你用这个背包装物品，最多能装的价值是多少？

举个简单的例子，输入如下：

1
2
3
N = 3, W = 4
wt = [2, 1, 3]
val = [4, 2, 3]

算法返回 6，选择前两件物品装进背包，总重量 3 小于W，可以获得最大价值 6。

解答

参考文章：https://labuladong.gitbook.io/algo/dong-tai-gui-hua-xi-lie/bei-bao-wen-ti

根据动态规矩的解题思路，首先应该明确三点：最优子结构、状态转移方程、重叠子问题。对于该题而言，状态为背包的重量，根据选择的物品的数量从而导致背包重量变化；对于每一个物品而言，每次有两个选择：装入背包、不转入背包，根据这一个特点可以总结出最优子结构为:max(‘装入背包’,’不转入背包’)。

这一步要结合对dp数组的定义和我们的算法逻辑来分析：

先重申一下刚才我们的dp数组的定义：

dp[i][w]表示：对于前i个物品，当前背包的容量为w时，这种情况下可以装下的最大价值是dp[i][w]。

如果你没有把这第i个物品装入背包，那么很显然，最大价值dp[i][w]应该等于dp[i-1][w]。你不装嘛，那就继承之前的结果。

如果你把这第i个物品装入了背包，那么dp[i][w]应该等于dp[i-1][w-wt[i-1]] + val[i-1]。

首先，由于i是从 1 开始的，所以对val和wt的取值是i-1。

而dp[i-1][w-wt[i-1]]也很好理解：你如果想装第i个物品，你怎么计算这时候的最大价值？换句话说，在装第i个物品的前提下，背包能装的最大价值是多少？

显然，你应该寻求剩余重量w-wt[i-1]限制下能装的最大价值，加上第i个物品的价值val[i-1]，这就是装第i个物品的前提下，背包可以装的最大价值。

综上就是两种选择，我们都已经分析完毕，也就是写出来了状态转移方程，可以进一步细化代码：

1
2
3
4
5
6
7
for i in [1..N]:
    for w in [1..W]:
        dp[i][w] = max(
            dp[i-1][w],
            dp[i-1][w - wt[i-1]] + val[i-1]
        )
return dp[N][W]

具体代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
    * 计算背包问题
    * 
    * @param n 物品数
    * @param w 背包可装载重量
    * @param wt 物品重量
    * @param val 物品价值
    * @return 最大价值
    */
   public int exec(int n, int w, int[] wt, int[] val) {
       // 二维数组:总物品数量；总物品重量
       int[][] dp = new int[n + 1][w + 1];
       dp[0][0] = 0;
       dp[1][wt[0]] = val[0];
       // 遍历物品
       for (int i = 1; i <= n; i++) {
           // 遍历重量，处理每个物品的对应每种情况下的最值,j代表背包可用重量
           for (int j = 1; j <= w; j++) {
               // 两种情况
               if (j - wt[i - 1] < 0) {
                   // 当前背包装不下这个物品
                   dp[i][j] = dp[i - 1][j];
               } else {
                   // 当前背包能装下这个物品
                   dp[i][j] = Math.max(dp[i - 1][j - wt[i - 1]] + val[i - 1], dp[i - 1][j]);
               }
           }
       }
       return dp[n][w];
   }